Mikromurtumamurtumateorian tukena, mitä suunnittelun esittelykirjassa yrität vihjailla, on Mohrin piirin seurauksia. Havainnollistamiseksi Wikipediasta:

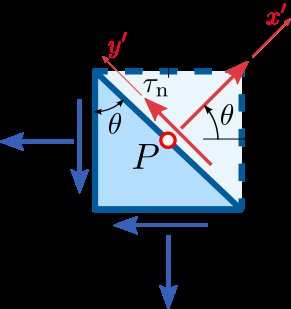
Kuten näette, kun sinulla on stressi x-suunnassa, stressi y- suuntaan ja leikkausjännitykseen, voit muuntaa jännityksen uudeksi mielivaltaiseksi akseliksi (x 'ja y'), jolla on erilainen normaali- ja leikkausjännitys. Perustoiminnot ratkaisevat nämä voimat:

$$ \ sigma_n = \ frac {1} {2} (\ sigma_x + \ sigma_y) + \ frac {1} {2} (\ sigma_x - \ sigma_y) \ cos 2 \ theta + \ tau_ {xy} \ sin 2 \ theta $$

$$ \ tau_n = - \ frac {1} {2} (\ sigma_x - \ sigma_y) \ sin 2 \ theta + \ tau_ {xy} \ cos 2 \ theta $$

Jos akseli on puhdas vääntö, yhtälöt yksinkertaistuvat:

$$ \ sigma_n = \ tau_ { xy} \ sin 2 \ theta $$$$ \ tau_n = \ tau_ {xy} \ cos 2 \ theta $$

Jos ensisijainen vikamenetelmä on leikkaushäiriö, kuten useimpien pallografiittimateriaalien tapauksessa , niin tämä tapahtuu, kun katsomme akselia, jossa $ \ theta = 0 $, ja jännitys on kokonaan leikkaus. Kuitenkin, jos katsomme akselia, jossa $ \ theta = 45 $ °, stressi on kaikki jännityksen normaalissa stressissä. Tässä tapauksessa, kun materiaali epäonnistuu helposti jännityksessä, se epäonnistuu tässä suunnassa.

Todellinen maailma on itse asiassa monimutkaisempi mikrohalkeamamurtumateorian, stoikastisten menetelmien ja väsymisstressin avulla. Suunnittelussa tämä on kuitenkin pidettävä mielessä - pelkkä leikkausjännitys ei tarkoita, että hauras materiaali pystyy käsittelemään vetovoimia. Konesuunnittelukirjan johdantona tämä on yksinkertaisesti saada sinut tietämään tämä ilmiö ja tietämään, että eron pitäisi olla. Tämän käsittelemiseksi tosielämässä hauraisiin materiaaleihin käytettäisiin suunnittelukriteerimenetelmiä, kuten Mohr-Coulombin teoria, kun taas sitkeisiin materiaaleihin käytetään von Misesin tuottokriteereitä. . Ryömintää käytetään muoveissa. Mukava yhteenveto muista menetelmistä on lueteltu Coloradon osavaltiossa.