Aluksi oletan, että kukin vaakasuorasta pinnastasi: työpöytä ja kolme itseäsi ovat kumpikin saman materiaalin. Naurettavan ja liioiteltujen tapausten käyttämiseksi vasen puoli, jos työpöytä ei ole raskasta marmoria, ja oikea puoli ei ole kevyttä balsa-puuta. Pöytä koostuu yhdestä yhtenäisestä materiaalista ja kukin itse on valmistettu omasta yhtenäisestä materiaalistaan: puu, lasi, metalli, lastulevy ja laminointi, vaneri, mikä tahansa.

Kuten on esitetty, kukin hyllyistä ja työpöydät on kiinnitetty itsenäisesti pystytukiin, jotka toimivat jalkoina. Näin ollen kunkin vaakasuoran pinnan paino siirretään suoraan pystytuille. Kaikki vaakasuorat pinnat ovat yhtenäisiä materiaaleja, joilla on tasainen painojakauma. Näin ollen kukin jalka kantaa puolet kaikkien vaakasuorien pintojen yhteispainosta.

Kummankin jalan osa, joka kokee koko sen yläpuolella olevan painon, on lyhyt osa kahden kolmionmuotoisen tukijalan välillä yksi työpöydälle ja toinen pöydän jalustalle / jalustalle.

Kummankin lyhyen jalkaosan rasitus on kunkin jalan kantama paino jaettuna jalan poikkileikkausalue z-taso (leveys jalan leveyden mukaan)

Työpöydän kannattimen kalteva osa kantaa osan työpöydän painosta. Kun taas työpöydän kannattimen lyhyessä pystysuorassa osassa on koko pystysuoran tuen paino työpöydän yläpuolella, kolme hyllyä ja osa työpöydän painosta. Kuinka suuri työpöydän painon osuus riippuu kohtisuorasta (normaalista) etäisyydestä pystytuesta.

Samoin jalan pohjassa kolmion muotoinen ahdin jakaa jalan kuormituksen uudelleen kolmion kokoonpanoon.

Tämä on vain yleiskatsaus siitä, miten ajattelet suunnitteluun liittyviä asioita. Kuten @Rick Teachey toteaa, sinun on todella suoritettava staattinen kurssi, haettava numerot painoille ja tuen poikkileikkaukselle ja liitettävä kaikki joihinkin kaavoihin.

Koska haluat tietää, mitä tapahtuu työpöydän kulmaan kohdistuvan kuormituksen kanssa, yksinkertaistan tämän kysymyksen kahteen ulottuvuuteen olettaen, että kulman jalka vastustaa yksinomaan kuormitusta. Ottaen huomioon, että teräsosien jäykkyys on suuruusluokkaa suurempi kuin puisen työpöydän, tämä ei todennäköisesti ole liian kaukana totuudesta.

Oletan myös, että työpöytä on valmistettu maagisista materiaaleista, joilla ei ole omaa painoa ja että työpöytä on muuten tyhjä muista kuormista, vain pitääkseen asiat yksinkertaisina. Lisäksi, kuten muut ovat maininneet, tämä on käytännössä mahdotonta tehdä ilman jonkin verran tietoa staattisuudesta. En voi antaa koko oppituntia täällä, mutta aion selittää asiat parhaalla mahdollisella tavalla.

Rakenne, jonka sinulla on käytännössä, on seuraava (työpöydän takapään poistaminen jalan jälkeen, mikä ei ole merkitystä, ja jalan pohjassa oleva lävistäjä, joka vain monimutkaistaa asioita eikä todellisuudessa muuta asiaankuuluvia sisäisiä rasituksia):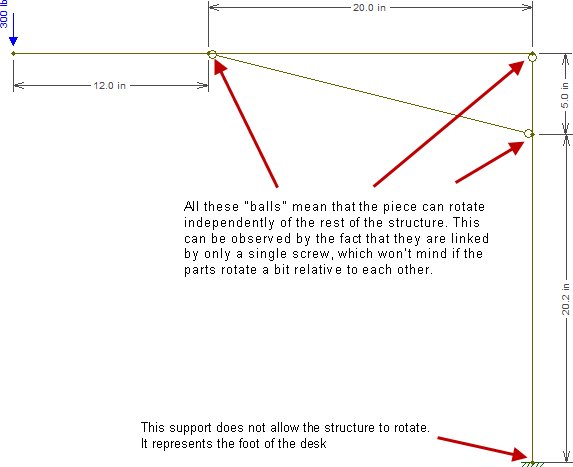

Tämä tapaus voidaan todella ratkaista käsin, joten tässä menee: Taulukon aivan reunan kuormitus on $ 300 \ text {lb} $ ja on $ 12 \ text {in} = 1 \ text {ft} $ diagonaalista. Tämä tarkoittaa, että säteen on kestettävä taivutusmomentti $ M = 300 \ cdot1 = 300 \ text {ft-lb} $ ja leikkausvoima, joka on yhtä suuri kuin sovellettu kuormitus $ Q = -300 \ text {lb} $ ( negatiivinen, koska se osoittaa alaspäin).

Olemme nyt kohdassa, jossa lävistäjä alkaa auttaa vaakapalkkia, joten meidän on selvitettävä, kuinka paljon voimaa kullekin heistä menee. Tätä varten meidän on katsottava hieman eteenpäin ja huomattava, että vaakasuora palkki kohtaa kolonnin toisessa kiinnitetyssä liitoksessa (ne "kuvassa olevat" pallot "). Nämä nivelet antavat osien kiertyä suhteessa toisiinsa, mikä (ja tämä on jotain, mitä opit staattisuudessa) tarkoittaa, että taivutusmomentti tässä kohdassa on nolla. Koska noissa $ 20 \ text {in} $: ssa (vaakasuoran palkin diagonaaliin ja sarakkeeseen liittyvän yhteyden välillä) ei ole muita ulkoisia kuormituksia, leikkausvoiman on oltava vakio kyseisellä venymällä. Ja koska leikkausvoima on taivutusmomentin johdannainen, momentin on vaihdeltava lineaarisesti. Ja koska lävistäjä on kiinnitetty ("pallo" -yhteys) vaakatasoon, se ei varastanut yhtään hetkeä. Tämä tarkoittaa, että vaakasäde siirtyy taivutusmomentista 300 diagonaalin alussa nollaan pylväässä. Jatkuva leikkausvoima tällä venymällä on siis sama kuin lineaarisen muunnoksen tangentti, joka on

$$ Q = \ dfrac {300 \ text {ft-lb}} {20 \ text {in} = \ frac {5} {3} ft} = 180 \ teksti {lb} $$.

Palaten siis takaisin vaakatason ja lävistäjän väliseen yhteyteen, tiedämme nyt, että vaakasäde siirtyi leikkausvoimasta $ -300 \ text {lb} $ arvoon $ + 180 \ text {lb} $. Tämä tarkoittaa, että diagonaalin on oltava kohdistanut pystysuuntaisen voiman, joka on yhtä suuri kuin $ + 480 \ text {lb} $ vaakatasoon. Koska lävistäjä on kiinnitetty molempiin päihin eikä siihen ole kohdistettu ulkoisia kuormia, se voi sisältää vain aksiaalisia kuormia. Tämä tarkoittaa, että nämä $ 480 \ text {lb} $ ovat itse asiassa vain osa diagonaalin tosiasiallisesti käyttämää voimaa. Vaakakomponentin voi helposti löytää tangentista, ja se on yhtä suuri kuin $ 480 \ cdot \ frac {20} {5} = 1920 \ text {lb} $. Lävistäjän aksiaalivoiman kokonaisvoiman voi löytää Pythogoras: $ \ sqrt {480 ^ 2 + 1920 ^ 2} = 1979 \ text {lb} $, ja se on pakattu . Sillä välin tämän voiman vaakakomponentti on pidätettävä vaakasuoralla säteellä, joka kärsii jännityksestä 1920 dollaria \ text {lb} $.

Nyt on jäljellä vain sarake. Koska vaakapalkki kärsii $ 1920 \ text {lb} $ -jännitteestä, sarakkeen on absorboitava se, mikä muuttaa jännitteen $ 1920 \ text {lb} $ -leikkaukseksi. Tämä leikkaus kuitenkin peruutetaan kytkemällä diagonaaliin, joka käyttää samaa voimaa (mutta toiselle puolelle, siis eri merkillä ... statics ). Näiden pisteiden välissä leikkaus on kuitenkin elossa ja hyvin. Ja missä on leikkaus, on taivutusmomentti. Jatkuva leikkaus $ 1920 \ text {lb} $ yli $ 5 \ text {in} $ tuottaa taivutusmomentin $ 1920 \ cdot \ frac {5} {12} = 800 \ text {ft-lb} $. Pylvään pohjan ja lävistäjän liitännän välillä ei enää ole leikkausta, joten momentti on vakio.

Vaakapalkin leikkaus oli myös $ + 180 \ text {lb} $, joka siirtyy sarakkeeseen aksiaalisena jännityksenä , jonka arvo on sama (sarakkeen sitä osaa venytetään) , ei squished!). Sen jälkeen kun yhteys diagonaaliin, joka myös kaataa sen vaakakomponentin $ -480 \ text {lb} $ (se oli ylhäällä positiivinen, koska se osoitti ylös. Täällä se osoittaa alas, joten se on negatiivinen). Siksi pylvään ja lävistäjän välillä sarake pakataan $ 300 \ text {lb} $, mikä on järkevää, koska kyseisen sarakkeen osan on kestettävä koko ulkoinen kuormitus, joka kohdistettiin taulukon reunaan. Jos sen pakkaus ei olisi yhtä suuri kuin käytetty kuorma, jokin olisi vialla.

Päivän lopussa päädyt rakenteeseen, joka käy läpi seuraavat (laajenna napsauttamalla):

Sisäisten voimien tunteminen ei kuitenkaan riitä tietämään, tukeeko työpöytäsi sitä. Se riippuu kuitenkin suuresti siitä, missä asut ja mitä koodeja sovelletaan (ja olen varma, että työpöytien ei tarvitse noudattaa rakennuskoodeja, mutta olen varma, että on olemassa asiaankuuluvia koodeja), eikä niihin voida vastata riittävästi täällä.

Tästä huolimatta jännitteisiin ja leikkauksiin liittyy yleensä vain vähän mysteeriä. Jännitystä varten jaa vetovoima poikkileikkauksen pinta-alalla ja vertaa sitä jännitystä teräksen lujuuteen (heikoin A500 on 45ksi) ja jossain varmuuskertoimessa (sallittu jännitysrakenne käyttää usein 60% teräksen lujuudesta). Leikkausta varten jaa leikkausvoima "leikkausalueella", joka on tapauksessasi yhtä suuri kuin poikkileikkausten "pystysuorien" sivujen pinta-ala. Tämä antaa sinulle leikkausjännityksen, jota tulisi verrata teräksen lujuuteen (sallittu jännitysrakenne käyttää 40% vetolujuudesta).

Taivutus ja pakkaaminen ovat kuitenkin mutkikkaampia johtuen taipumisriskistä, ja ne on tehtävä asiaankuuluvilla koodeilla. Jos joku sivuuttaa taipumisen ( oikeastaan ​​ ei pitäisi), niin kyse on vain asiaankuuluvan stressin saamisesta ja sen vertaamisesta uudelleen voimaan. Pakkauksessa se on sama kuin jännityksessä. Taivutusta varten jaa taivutusmomentti kimmomoduulilla, jotta saat maksimaalisen jännityksen / puristusjännityksen (katso alla) ja vertaa myös sallittuun jännitykseen:

$$ \ sigma = \ dfrac {6Mh_1} { b_1h_1 ^ 3-b_2h_2 ^ 3} $$

Ja mitä kannattaa, jalan pohjan lävistäjä voi olla merkityksellinen vääntymisanalyysissä, vaikka jos minun piti arvata, sanoisin vaakasuoraa palkkia tukeva ylempi diagonaali olisi ohjaava elin (vääntymistä varten).

Kysymyksesi on staattinen analyysi tai oikeastaan ​​jotain, jonka insinööri oppii "Materiaalimekaniikan" kurssilla. Sinun on tiedettävä, kuinka paljon rasitusta työpöydän jäsenille aiheutuu 300 lb: n voimasta ja voiko se pitää kuormaa.

Olen ratkaissut tämän ongelman pöydän poikkipalkkitukeen. Suurin kuormitus näkyy kuitenkin tukielimessä, kun kuorma on suoraan sen yläpuolella eikä kuorman lopussa.

Analyysi voidaan suorittaa muille jäsenille, mutta perusteellisen analyysin tekemiseksi sinun on tarkasteltava yhteyspisteitä, koska ne olisivat todennäköisiä tukehtumispisteitä.

Linkitetty asiakirja Edellä mainittu tehtiin kehitettävällä alustalla nimeltä CADWOLF. Voit muuttaa kuormaa nähdäksesi tuloksena olevat voimat.

Asiakirjassa kuvataan voimien ja momenttien yhteenlaskeminen näiden tulosten saamiseksi. Tätä samaa prosessia voidaan käyttää poikkipalkin kuormitusten ja reaktiovoiman kanssa pystysuorien jalkojen alempiin vaakasuoriin jakoihin yhdistävän poikkipalkin kuormituksen laskemiseksi.

Sain ilmaisen 3 vuoden opiskelijaversion Autodesk Inventorista (koska tunnen sen myös SolidWorks, CATIA, toimivat). Malli sitten työpöytä ja suorita staattinen analyysi. A0-arkkien voimakaaviot ovat jo kauan menneet.